（e）衝撃的な空気圧力

図−5.1の通り長さL0、断面積Aのシリンダ内に1気圧15℃の空気が満たされているとする。シリンダの左側にはピストンがあり、最初はシリンダとピストンの間にはわずかの隙間があるが、次の瞬間ピストンが右側に移動してシリンダを密閉し、Δt秒（＜2L0/a1）の間にピストンの速度がvになったとする。このピストンの移動によりシリンダ内の空気は圧縮され、衝撃的な圧力が発生する。但しa1は音速（＝341m/s：15℃）である。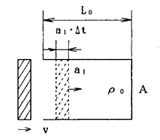

図-5.1　衝撃的な空気圧力

ピストンの押した力Fは運動量の変化となり、圧力の変化となるから、空気の密度をρ0（＝0.125kg/m3）とすると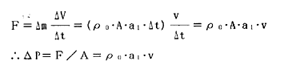

海水の上昇速度vは、波形が正弦波であるならば振幅をA1、角速度をω1とすると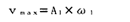

で現すことが出来る。角速度ω＝2π/Tであるが、有義波の1周期には2次以上の高調波が含まれているので、今、仮にω1＝3×2π/Tとし、Hmax＝1.8×H1/3とすると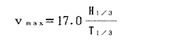

故に、衝撃的な空気圧力Plは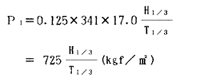

となる。

空気室に薄肉圧力容器の理論を適用すれば、この圧力により空気室に働く引張応力σ0は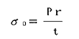

である。日本周辺海域における最高波は1987年10月17日御坊沖で観測され、その時のHl/3＝11.37m,Tl/3＝13.8sであった。r＝1070mm、t＝9mmとすると

σ0＝0.1kgf/mm2であり、SUS316Lの短期の許容引張応力21kgf/mm2に対して充分ゆとりがある。

前ページ　　　目次へ　　　次ページ